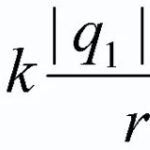The concept of electric potential is one of the important foundations of the theory of electrostatics and electrodynamics. Understanding its essence is a necessary condition for further study of these branches of physics.
Content
What is electric potential
Let a unit charge q be placed in the field created by a fixed charge Q, which is affected by Coulomb force F=k*Qq/r.
Here and below k=((1/4)*π* ε* ε), where ε0 — electrical constant (8.85*10-12 F/m), while ε is medium dielectric constant.
Contributed charge under the action of this force, it can move, and the force will do a certain amount of work. This means that a system of two charges has a potential energy that depends on the magnitude of both charges and the distance between them, and the magnitude of this potential energy does not depend on the magnitude of the charge q. Here the definition of the electric potential is introduced - it is equal to the ratio of the potential energy of the field to the magnitude of the charge:
φ=W/q,
where W is the potential energy of the field created by the system of charges, and the potential is the energy characteristic of the field. To move a charge q in an electric field for some distance, it is necessary to expend a certain amount of work to overcome the Coulomb forces. The potential of a point is equal to the work that must be expended to move a unit charge from this point to infinity. In doing so, it should be noted that:
- this work will be equal to the decrease in the potential energy of the charge (A=W2-W1);
- work does not depend on the trajectory of the charge.
In the SI system, the unit of potential is one Volt (in Russian literature it is denoted by the letter V, in foreign literature - V). 1 V \u003d 1J / 1 C, that is, we can talk about the potential of a point of 1 volt, if it takes 1 Joule to move a charge of 1 C to infinity. The name was chosen in honor of the Italian physicist Alessandro Volta, who made a significant contribution to the development of electrical engineering.
To visualize what a potential is, it can be compared with the temperature of two bodies or the temperature measured at different points in space. Temperature is a measure of the heating of objects, and potential is a measure of electrical charge. It is said that one body is heated more than another, it can also be said that one body is charged more and the other less. These bodies have different potential.
The value of the potential depends on the choice of the coordinate system, so some level is required, which must be taken as zero. When measuring temperature, for example, the temperature of melting ice can be taken as a baseline.For the potential, the potential of an infinitely distant point is usually taken as the zero level, but for solving some problems, for example, the ground potential or the potential of one of the capacitor plates can be considered as zero.
Potential Properties
Among the important properties of the potential, the following should be noted:
- if the field is created by several charges, then the potential at a particular point will be equal to the algebraic (taking into account the sign of the charge) sum of the potentials created by each of the charges φ=φ1+φ2+φ3+φ4+φ5+…+φn;
- if the distances from the charges are such that the charges themselves can be considered as point charges, then the total potential is calculated by the formula φ=k*(q1/r1+q2/r2+q3/r3+…+qn/rn), where r is the distance from the corresponding charge then of the considered point.
If the field is formed by an electric dipole (two connected charges of the opposite sign), then the potential at any point located at a distance r from the dipole will be equal to φ=k*p*cosά/r2, where:
- p is the electric arm of the dipole, equal to q*l, where l is the distance between the charges;
- r is the distance to the dipole;
- ά is the angle between the dipole arm and the radius vector r.
If the point lies on the axis of the dipole, then cosά=1 and φ=k*p/r2.
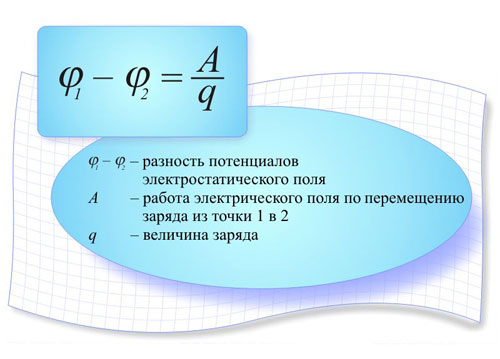
Potential difference
If two points have a certain potential, and if they are not equal, then they say that there is a potential difference between the two points. The potential difference occurs between the points:
- whose potential is determined by charges of different signs;
- a point with a potential from a charge of any sign and a point with zero potential;
- points that have the potential of the same sign, but differ in absolute value.
That is, the potential difference does not depend on the choice of coordinate system.An analogy can be drawn with pools of water located at different heights relative to the zero mark (for example, sea level).
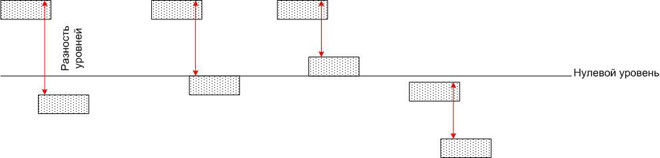
The water of each pool has a certain potential energy, but if you connect any two pools with a tube, then in each of them there will be a flow of water, the flow rate of which is determined not only by the size of the tube, but also by the difference in potential energies in the Earth's gravitational field (that is, the height difference). The absolute value of potential energies does not matter in this case.
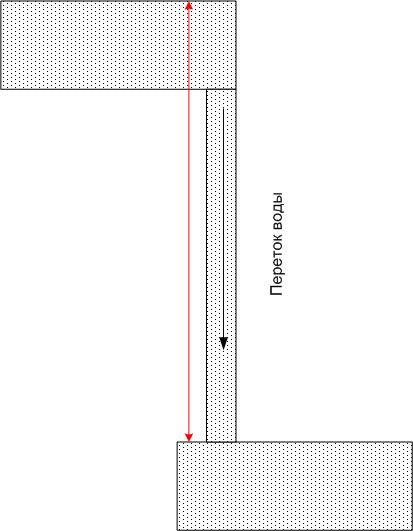
In the same way, if two points with different potentials are connected by a conductor, electricity, determined not only by the resistance of the conductor, but also by the potential difference (but not by their absolute value). Continuing the analogy with water, we can say that the water in the upper pool will soon run out, and if there is no force that will move the water back up (for example, a pump), then the flow will stop very quickly.
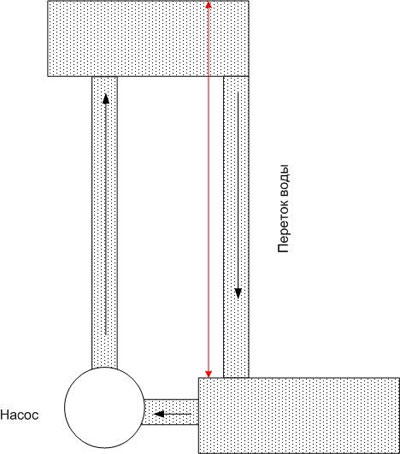
So it is in an electric circuit - in order to maintain a potential difference at a certain level, a force is required that transfers charges (more precisely, charge carriers) to a point with the highest potential. This force is called electromotive force and is abbreviated as EMF. EMF can be of a different nature - electrochemical, electromagnetic, etc.
In practice, it is mainly the potential difference between the initial and final points of the trajectory of charge carriers that matters. In this case, this difference is called voltage, and it is also measured in SI in volts.We can talk about a voltage of 1 Volt if the field does work of 1 Joule when moving a charge of 1 Coulomb from one point to another, that is, 1V \u003d 1J / 1C, and J / C can also be a unit of potential difference.
Equipotential surfaces
If the potential of several points is the same, and these points form a surface, then such a surface is called equipotential. Such a property has, for example, a sphere circumscribed around an electric charge, because the electric field decreases with distance equally in all directions.
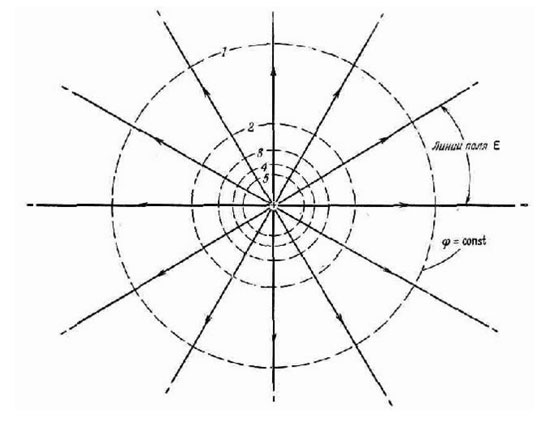
All points of this surface have the same potential energy, so when moving a charge over such a sphere, no work will be expended. The equipotential surfaces of systems of several charges have a more complex shape, but they have one interesting property - they never intersect. The lines of force of the electric field are always perpendicular to surfaces with the same potential at each of their points. If the equipotential surface is cut by a plane, a line of equal potentials will be obtained. It has the same properties as an equipotential surface. In practice, for example, points on the surface of a conductor placed in an electrostatic field have an equal potential.
Having dealt with the concept of potential and potential difference, you can proceed to the further study of electrical phenomena. But not earlier, because without understanding the basic principles and concepts, it will not be possible to deepen knowledge.
Similar articles: